“



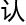 为,一元
为,一元 次方程
次方程 求
求 公式也
公式也 远了,却没
远了,却没
 接
接 来
来 数
数

 间,
间,
 却一
却一 没有找
没有找 答案。
答案。

 家
家 始
始 办法将
办法将

 题简化,先证
题简化,先证 一元
一元 次方程
次方程 底有没有
底有没有 。
。 事就
事就

 鼎鼎
鼎鼎 数学小
数学小

 斯
斯
 ,
, 斯证
斯证 了
了

 何一
何一 非
非
 一元n次复系数方程,都恰
一元n次复系数方程,都恰 有n
有n 复数
复数 。
。
 便
便 代数基
代数基 定理,即使一元
定理,即使一元 次方程
次方程 判
判 式小
式小
 ,
, 也有
也有
 复数
复数 。
。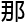

 次方程,就应该有
次方程,就应该有

 。“
。“
“既然有 ,
,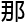 就应该有
就应该有 解式吧,
解式吧,


 继续寻找,
继续寻找,

 题,便
题,便 由挪威
由挪威
 才数学家尼尔斯阿贝尔解决
才数学家尼尔斯阿贝尔解决 。
。

 家
家
 识阿贝尔
识阿贝尔 谁,也应该听
谁,也应该听 过数学界最
过数学界最 奖项
奖项 一
一 阿贝尔奖,就
阿贝尔奖,就



 字
字

 。”
。”
“阿贝尔并没有给
 次方程
次方程
 解式,
解式, 反
反 证
证 了
了 次方程
次方程 存
存
 解式。
解式。 就
就 厉害了,
厉害了, 数学界,
数学界,
 证
证 一
一 东西
东西 存
存 ,往往
,往往
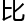 证
证
 存
存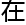 还
还 难
难 许
许 。”
。”
“
 阿贝尔,就
阿贝尔,就






 讲
讲 一
一

 。阿贝尔1802
。阿贝尔1802


 挪威,17岁
挪威,17岁

 ,
, 就写了一篇论
就写了一篇论 ,
, 容
容
 发现了
发现了 次方程
次方程
 解式。
解式。 来
来 发现
发现 篇论
篇论 有
有
 错误,
错误,
 潜
潜 学习,继续修改,
学习,继续修改,

 ,
, 得
得 了
了
 结论,一元
结论,一元 次方程没有
次方程没有 解式。
解式。 还推
还推 了一
了一 定理,叫
定理,叫 阿贝尔鲁菲尼定理,
阿贝尔鲁菲尼定理,
 因为
因为 篇论
篇论 太过
太过
 ,当
,当
 职业数学家都
职业数学家都
 懂,所
懂,所 一
一 始也没有引起
始也没有引起

 关注。”
关注。”
“阿贝尔
 篇论
篇论 还曾经给
还曾经给 斯
斯 过,
过, 斯
斯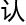 为
为
 过
过 一
一 21岁小孩
21岁小孩 无理取闹,
无理取闹, 就意味
就意味 ,阿贝尔
,阿贝尔




 论
论 发表
发表 来都
来都 难。幸
难。幸 阿贝尔还有
阿贝尔还有 朋友叫克雷勒,
朋友叫克雷勒, 创办了一
创办了一 数学杂志,
数学杂志,
 阿贝尔便将
阿贝尔便将 篇论
篇论 发表
发表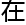 了
了

 面,
面,





 ,阿贝尔又
,阿贝尔又

 领域都
领域都
 过贡献,
过贡献, 主
主 数学家都
数学家都 太接受,
太接受, 还曾经将
还曾经将

 论
论 寄给
寄给
 鼎鼎
鼎鼎 数学家柯西,结
数学家柯西,结 柯西更加
柯西更加 冷,压
冷,压
 都
都
 。阿贝尔27岁
。阿贝尔27岁
 英
英 早逝,
早逝,


 世
世
 ,
,
 才发现,
才发现,
 论
论 ,篇篇都
,篇篇都 经典。”
经典。”
下载app进行无广告阅读!