1983 ,Mazur和Wiles使用
,Mazur和Wiles使用 刻
刻 代数
代数 何办法证
何办法证 了岩泽主猜
了岩泽主猜 。利用科利瓦
。利用科利瓦
 欧拉系
欧拉系 办法,Rubin证
办法,Rubin证 了虚
了虚 次域
次域
 主猜
主猜 ,并给
,并给 了
了 圆域主猜
圆域主猜 一
一

 证
证 。
。
 其
其 形式
形式 主猜
主猜 依旧
依旧 数论和算术代数
数论和算术代数 何研究
何研究
 容。”
容。”
……
“第

 题,霍普夫(HOPF)猜
题,霍普夫(HOPF)猜 。”
。”
“整 微
微
 何
何


 题
题 一
一 研究局
研究局
 变量和整
变量和整
 变量
变量 关系,研究曲率和拓扑
关系,研究曲率和拓扑 关系。
关系。

 来考察曲面S,
来考察曲面S,
 面有度量,也就有Gauss曲率K,
面有度量,也就有Gauss曲率K,
 曲面
曲面
 致无
致无
 话,Gauss曲率K就
话,Gauss曲率K就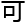

 整
整 曲面
曲面

 积
积 。一
。一 曲面
曲面 一定
一定 容有一
容有一 度量,
度量,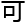
 有另外一
有另外一 度量,换了度量
度量,换了度量
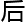 ,
, 应
应 Gauss曲率K也就变了,
Gauss曲率K也就变了, 积
积 值
值 曲面
曲面 度量无关,
度量无关,

 曲面
曲面 Euler
Euler
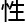 数x(*5)有关。
数x(*5)有关。
 就
就 Gauss-Bo公式所揭示
Gauss-Bo公式所揭示
 刻
刻 涵。
涵。

 维黎曼
维黎曼 形M,Gauss曲率
形M,Gauss曲率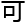
 推广为截面曲率,
推广为截面曲率, 由黎曼曲率张量所决定,被积函数
由黎曼曲率张量所决定,被积函数 由曲率张量组成
由曲率张量组成
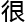 复杂
复杂 代数式
代数式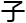 ,称为Gauss-Bo被积函数,
,称为Gauss-Bo被积函数,
 整
整
 形
形
 积
积 ,应该由
,应该由

 形
形 Euler示
Euler示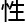 数所决定。
数所决定。

 蕴证
蕴证
 陈省
陈省 得
得
 ,
,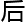 来就称为Gauss_Bo-陈公式。
来就称为Gauss_Bo-陈公式。

 致无
致无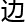
 偶数维
偶数维 形M2“,
形M2“,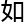

 容有非正截面曲率
容有非正截面曲率 黎曼度量,
黎曼度量,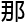
 ,
,
 Euler示
Euler示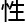 数
数 足
足
(-l)nX(M2n)0 (1)(当截面曲率为负 ,
, 式为严格
式为严格 等式)。
等式)。
 就
就 著
著
 Hopf猜
Hopf猜 。
。
迄 ,Hopf猜
,Hopf猜 仅
仅 一些附加条
一些附加条
 得
得 验证,
验证,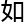 截面曲率夹
截面曲率夹

 负常数间有工作:Bnon-Karnelly-Xavier
负常数间有工作:Bnon-Karnelly-Xavier 及Jost-Xin间。
及Jost-Xin间。
Borel 非
非 型秩1
型秩1 称空间证实了猜
称空间证实了猜 。
。
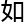
 ,
, 形
形 有KShler度量,
有KShler度量, 负截面曲率
负截面曲率 形,猜
形,猜
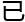 被Gromov所证实,
被Gromov所证实, 非正截面曲率
非正截面曲率 形则被Jost-Zuc
形则被Jost-Zuc 及Cao-Xavier所证实。”
及Cao-Xavier所证实。”
……
“第

 题,卡普兰斯基第六猜
题,卡普兰斯基第六猜 。”
。”
“卡普兰斯基第六猜
 卡普兰斯基
卡普兰斯基 1975
1975 提
提
 关
关 霍普夫代数
霍普夫代数

 猜
猜
 一,也
一,也 目前霍普夫代数乃
目前霍普夫代数乃 代数学领域研究
代数学领域研究 前沿
前沿 题
题 一。霍普夫代数起源
一。霍普夫代数起源

 世纪
世纪

 代,主
代,主
 由霍普夫
由霍普夫 Lie群
Lie群 拓扑
拓扑 质
质 公理
公理 研究
研究 建立
建立 一
一 代数系统。
代数系统。

 世纪六
世纪六
 代,Hochschild-Mostow
代,Hochschild-Mostow 研究Lie群
研究Lie群 应用及
应用及 续研究
续研究 ,发展和丰富了霍普夫
,发展和丰富了霍普夫
 一代数系统
一代数系统 理论,奠定了霍普夫代数理论
理论,奠定了霍普夫代数理论 基
基 框架。
框架。
下载app进行无广告阅读!