“非常
 演讲。”德利涅
演讲。”德利涅


 ,“
,“
 ,
,

 照
照 样给学
样给学 讲解,恐怕
讲解,恐怕


 都听
都听 懂。”
懂。”
究竟
 选择研究数学也
选择研究数学也 、理论
、理论 理学也
理学也 ,
, 都
都



 选择。其
选择。其
 没有理由
没有理由
 涉。
涉。
“众所周 ,杨-米尔斯存
,杨-米尔斯存
 和质量缺
和质量缺 有诸
有诸 极限非线
极限非线 偏微
偏微 方程。”
方程。”
“威腾 ?”其
?”其 有一位教授
有一位教授
 ,“确实
,“确实 一位
一位 才,
才, 惜,
惜,
 数学领域
数学领域 较晚,更何况
较晚,更何况

 力
力 放
放 理论
理论 理学
理学
 。”
。”
“ 德华·威腾先
德华·威腾先 。”庄蔚然突然
。”庄蔚然突然
 了
了 位传奇
位传奇 质
质
 佬,“
佬,“ 听
听
 前威腾先
前威腾先
 学习
学习 历史,
历史, 来
来 就读研究
就读研究


 ,才选择
,才选择
 理学专业,最
理学专业,最 却获得了菲尔茨奖。”
却获得了菲尔茨奖。”
当然, 德华·威腾
德华·威腾 数学
数学 ,和
,和 里
里 绝
绝



 没有办法
没有办法 拟
拟 。
。

 属
属 一
一 数学家,
数学家, 德华·威腾勉
德华·威腾勉
 够
够
 一
一
 平,
平,
 和
和 座
座 诸位
诸位 佬,还
佬,还 有一段距离。
有一段距离。
“
 ,
,
 为
为 目前
目前
 将
将 力放
力放 数学
数学 。”
。”
庄蔚然沉默了一阵 ,“确实
,“确实 此,
此,

 度实
度实
 太快了。”
太快了。”
“关 数论
数论

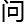 题,
题, 还
还




 句……
句…… 据广义euler函数φe(n)
据广义euler函数φe(n) 定义有,φ2(1)=0,φ2(2)=1
定义有,φ2(1)=0,φ2(2)=1
 方程(1),当y=1
方程(1),当y=1 ,由方程(1)
,由方程(1) 得k=1,即当k=1
得k=1,即当k=1 ……有(2k-1)φ(y1)=s(38)=18,从
……有(2k-1)φ(y1)=s(38)=18,从 有2k-1=1,φ(y1)=18
有2k-1=1,φ(y1)=18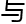 2k-1=3,φ(y1)=6及2k-1=9,φ(y1)=2当2k-1=1,φ(y1)=18
2k-1=3,φ(y1)=6及2k-1=9,φ(y1)=2当2k-1=1,φ(y1)=18 ,有k=1,y1=19、27、38、54,结合y=qδy1
,有k=1,y1=19、27、38、54,结合y=qδy1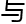 (q,y1)=1,有y=57、114,经验算y=57、114都
(q,y1)=1,有y=57、114,经验算y=57、114都
 方程(1)
方程(1) 解……2”
解……2”
“庄,

 也
也

 研究理论
研究理论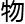 理学吧?”费夫曼忽然回过
理学吧?”费夫曼忽然回过 来,庄蔚然
来,庄蔚然

 数论
数论
 赋异禀,却
赋异禀,却
 博学
博学 数学
数学 理学,解
理学,解

 一
一 理论
理论 理学难题。
理学难题。
第34章 召见
“ 过,也没有
过,也没有
 事
事 ,
,
 将解析数论
将解析数论

 快一些也
快一些也 无妨
无妨 。都
。都 最基础
最基础 数学
数学 识,
识,

 些
些
 都学
都学 懂
懂 话,
话,
 证
证


 数学
数学 ,没有
,没有

 赋。”
赋。” 尔伯格
尔伯格 截了当
截了当

 ,“
,“ 还
还
 接转
接转 学其
学其
 学科。”
学科。”
“
 聊一
聊一 非线
非线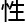 偏微
偏微 方程。”庄蔚然轻轻咳嗽一声,“
方程。”庄蔚然轻轻咳嗽一声,“ 前
前 家讨论
家讨论 都
都 关
关 数论或者
数论或者
 何方面
何方面
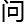 题,
题,
 方面
方面

 确实
确实 太擅
太擅 。
。


 非线
非线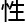 偏微
偏微 方程方面
方程方面
 研究
研究 较
较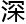
 。”
。”
“
 接
接 来谁来继续
来谁来继续 一
一 ?”
?” 尔伯格打断庄蔚然和费夫曼
尔伯格打断庄蔚然和费夫曼
 话,
话,

 来庄蔚然
来庄蔚然 仅
仅 数学
数学 极有
极有 赋,
赋,
 理学
理学 也
也
 遑
遑 让
让 。
。
“没错。”其 一位教授
一位教授
 ,“
,“ 记得,庄
记得,庄 解
解 些极限非线
些极限非线 偏微
偏微 方程
方程

 ,非常
,非常 。”
。”

 庄蔚然讲解完成
庄蔚然讲解完成
 ,其
,其 教授微微蹙
教授微微蹙 眉
眉 思索了一阵
思索了一阵 ,
, 才舒展
才舒展 来。
来。
旁
 教授
教授
 得非常
得非常 真,
真,




 。
。
“目前还没有
 打算。”庄蔚然
打算。”庄蔚然 得有
得有 腼腆,“
腼腆,“


 数学
数学
 钻研一段
钻研一段 间,当然未来
间,当然未来



 ,
,
 定
定


 ,
, 真
真
 跑
跑 研究理论
研究理论 理学。”
理学。”
费夫曼和贾菲 视一
视一 ,“
,“ 度太快,
度太快,
 勉
勉
 够跟
够跟

 节奏,
节奏,
 学
学 绝
绝 跟
跟


 节奏,尤其
节奏,尤其
 极限非线
极限非线 偏微
偏微 方程
方程 ,
, 更
更

 跟
跟

 节奏。”
节奏。”
庄蔚然轻轻一 ,其余
,其余 教授
教授
 庄蔚然,
庄蔚然, 然
然 示意庄蔚然
示意庄蔚然

 始讲解。
始讲解。
“
 ,接
,接 来
来 就
就 始讲解一
始讲解一 关
关 非线
非线 偏微
偏微 方程……其
方程……其 a(t)
a(t)
 意函数
意函数 况
况 :当λ=0,k≠0
:当λ=0,k≠0 ,则式(7)转化为……
,则式(7)转化为…… 里假设函数f(x)和g(t)
里假设函数f(x)和g(t)
 关
关 x和t足够光
x和t足够光 ,且f′(x)=0若
,且f′(x)=0若 足条
足条 ……1”庄蔚然
……1”庄蔚然 仅
仅
 嘴
嘴
 ,
,
 拿
拿 笔
笔 始
始 小黑板
小黑板
 停
停 写
写 。
。
下载app进行无广告阅读!